This is an attempt to convey a method to do encrypted search to non-cryptographers. Please excuse the lack of rigour for which I will compensate at the end of the article.

Assume you have a public key encryption system.

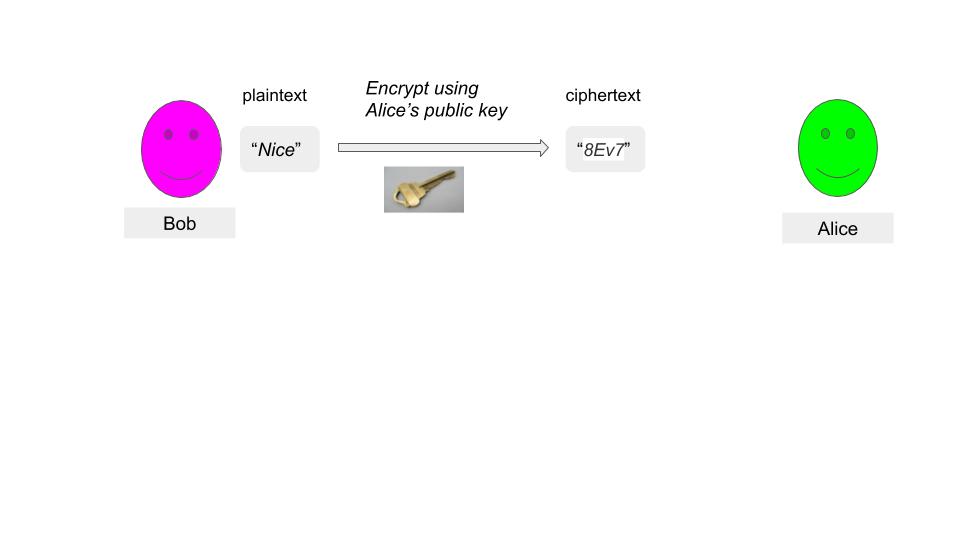
Bob is sending an encrypted message to Alice using Alice’s public key

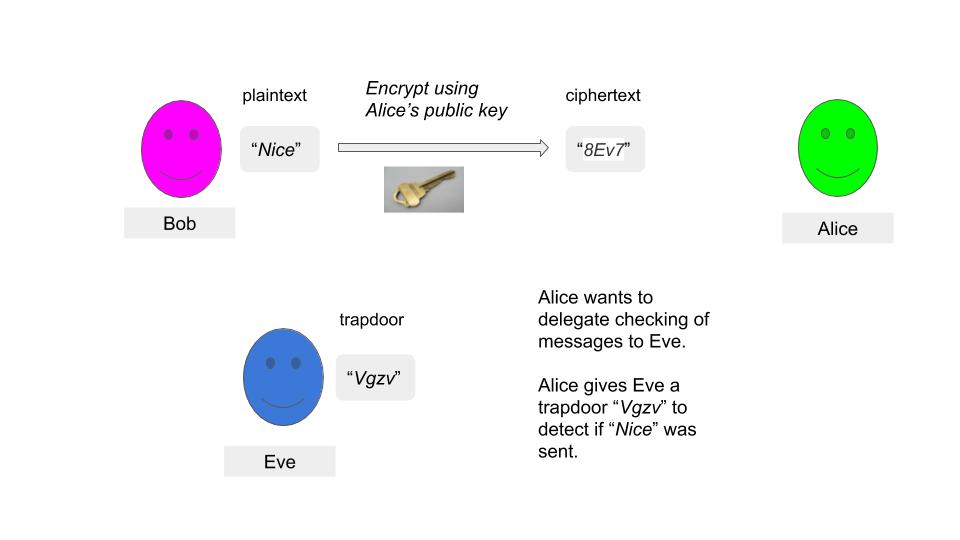
Alice wants to delegate some checking of messages to Eve. She wants Eve to check if the encrypted message is her favourite keyword “Nice”, but she does not want Eve to know she is looking for “Nice”.

How can Eve verify that “8Ev7” is actually “Nice” in encrypted form ? What you need here is an auxiliary string called a trapdoor which Eve can use to verify the equality.

Encrypting the trapdoor produces the original ciphertext, allowing Eve to verify equality.

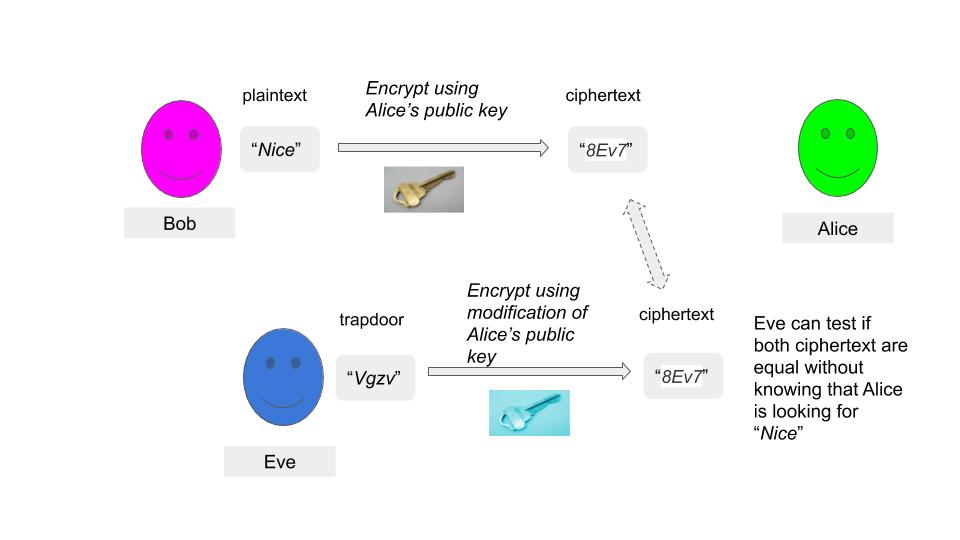
The trapdoor can be produced using a bilinear map which enables two different ways of producing same ciphertext.

A bilinear map is a function of two variables f(x, y) satifying this condition

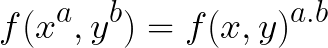
Let “x” be the text to be encrypted. The encrypted text will be generated by applying f(x, y) where “y” is the key combination (g^{ra}) as shown below.

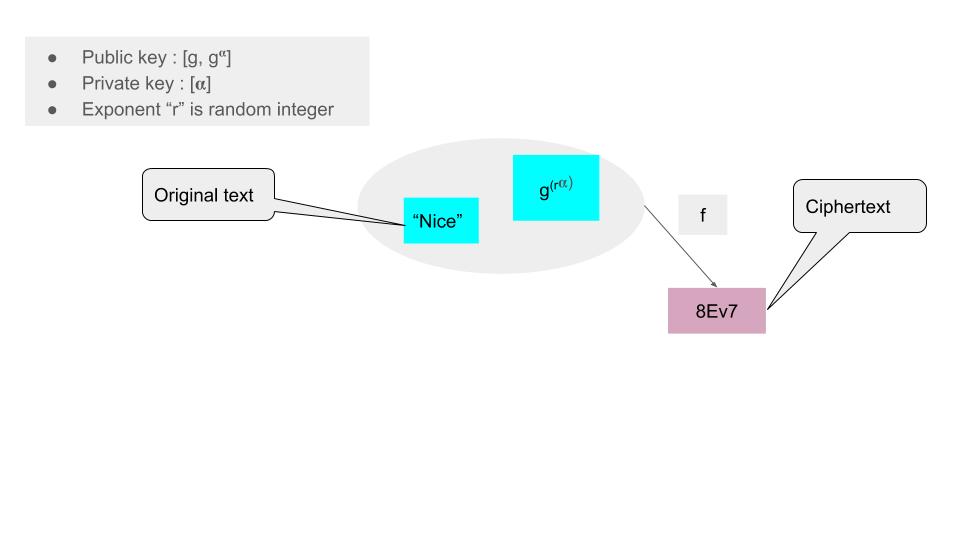
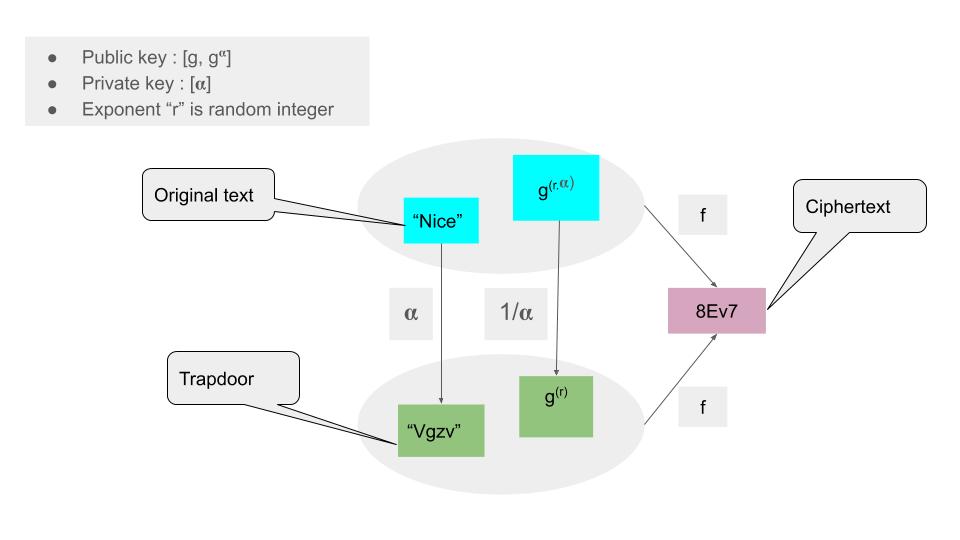
Next, you have to generate two more items

1. an auxiliary string called the trapdoor in the form of original text raised to power of (Alpha)
2. a mangled public key, produced from original public key by raising to power of (1/Alpha)

as shown in the lower shaded circle

Now by the property of a bilinear map, the exponentiation by (Alpha) and (1/Alpha) cancels as shown here

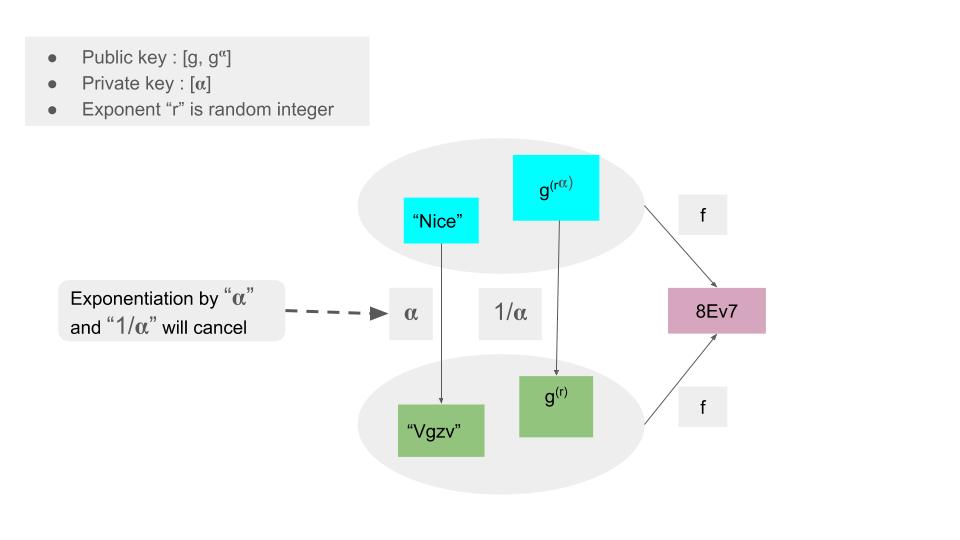
As a result, we now have two ways of producing the same encrypted text.

A third-party which has the trapdoor “Vgzv” can test if the encrypted text (“8Ev7”) is the string being searched for.

This is intuitively the cryptographic construction given by Boneh, et al in Sec 3.1 of their paper[1]

I have played fast and loose here to provide intuition. Refer to original paper for rigorous explanation.

How to produce bilinear maps ?

I am not going into that here. You have to use Weil pairings or Tate pairings over elliptic curves.

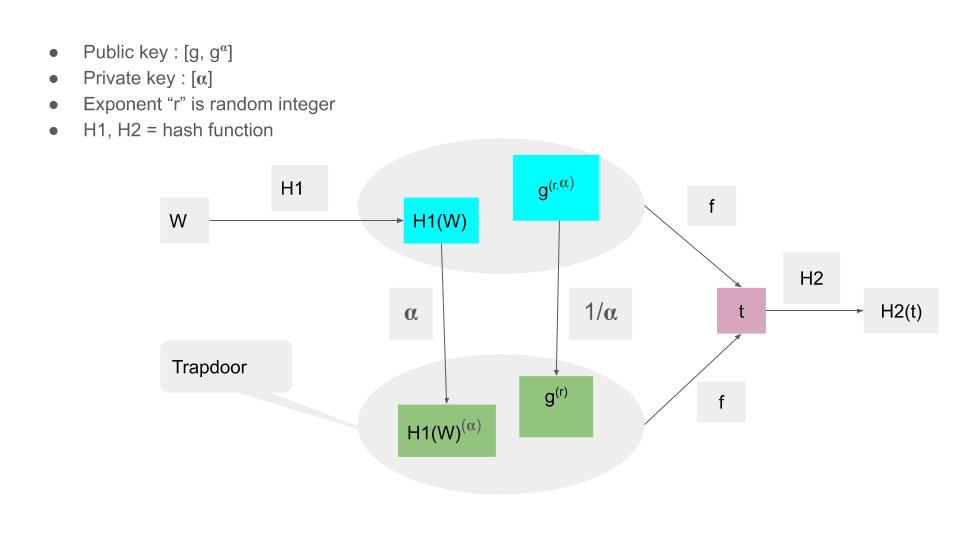
Diagram of the full construction

There are two more hash functions which come into play in the complete scheme.

Reference

1. Boneh, et al. Public Key Encryption with keyword Search. https://crypto.stanford.edu/~dabo/pubs/papers/encsearch.pdf
2. Alfred Menezies. An introduction to pairing-based cryptography (2005) http://www.math.uwaterloo.ca/~ajmeneze/publications/pairings
3. John Bethencourt. Intro to bilinear maps https://people.csail.mit.edu/alinush/6.857-spring-2015/papers/bilinear-maps.pdf
4. Advantages of bilinear map. https://crypto.stackexchange.com/questions/12357/advantages-of-bilinear-map4”>